Extensive statistical analysis of the variability of concrete rebound hardness based on a large database of 60 years experience

Paper published in Construction and Building Materials 53 (2014) 333-347

http://dx.doi.org/10.1016/j.conbuildmat.2013.11.113 

Authors: Katalin Szilágyi PhD, Adorján Borosnyói PhD, István Zsigovics PhD

Keywords: Concrete, non-destructive testing, rebound index, repeatability, statistical characteristics

Abstract: Non-destructive testing methods for concrete structures require statistical validation of reliability model parameters. Present paper studies a comprehensive database of several thousand test locations for the better understanding of the statistical characteristics of rebound hardness of concrete and highlights that several gaps are found both in current technical literature and standardisation. Detailed evaluation is provided on repeatability and influencing parameters. Results of statistical analyses are presented for the within-test standard deviation, coefficient of variation, range and studentized range of rebound indices. Indications for the reconsideration of particular statements in the technical literature and standards are given.

1. Introduction

During the design of reinforced concrete structures the designer specifies the strength class of concrete that is taken into account. The same is carried out if the performance of the concrete is determined by in-situ testing, e.g. surface hardness testing for strength assessment. The designer’s assumption should recognise the variability of concrete as a structural material and the designer specifies the design strength of the concrete using its characteristic compressive strength that covers the variability of the strength of concrete [1]. The characteristic strength is based on statistical concepts and usually means a limit value of strength below which no more than 5% falls from test results of a chosen concrete mix or a structure. This concept is illustrated in Fig. 1a which sketches a histogram of concrete strengths that can correspond to a particular series of tests and how the test results could be approximated by e.g a normal distribution density function. Fig. 1b shows the idealized normal distribution density function that is usually assumed in design and in quality control based on statistical methods. The lower limit indicated in the diagram is the characteristic strength (f_ck) below which no more than an acceptably chosen part of the strength tests values shall fall. The characteristic strength is usually given as a function of the mean strength, the standard deviation of the strength and an appropriate margin parameter that covers the type of the probability distribution of strength (that is not necessarily always normal distribution), the level of the percentile (that is not necessarily always 5%) and the reliability of the strength approximation (that is depending on the available number of test results) in the following form: f_ck = f_cm – k×s; where f_cm = mean strength, k = margin parameter and s = standard deviation of strength. The same can be formulated if one introduces the coefficient of variation for the strength as: f_ck = f_cm×(1– k×V); where V = coefficient of variation for the strength and the further parameters are the same as before.

Fig. 1. a)     Frequency histogram of concrete strength with the best fit probability density function

Fig. 1. b)     Idealized normal probability density function of concrete strength

Reliability analysis techniques mostly concentrate on the use of the coefficient of variation for taking into account the variability of different material characteristics, rather than the standard deviation. Whether the standard deviation or the coefficient of variation is the appropriate measure of dispersion for concrete strength depends on which of the two measures is more nearly constant over the range of the strength [2]. Technical literature indicates that the coefficient of variation is considered to be more applicable for within-test evaluations [2], however, the standard deviation remains reasonably constant over a wide range of strengths [3]. Fig. 2 illustrates the standard deviation and the coefficient of variation of concrete strength having the average compressive strengths in the range of 20 to 70 MPa, based on literature data [4].

Fig. 2. a)     Standard deviation of the compressive strength of concrete [4]

Fig. 2. b)     Coefficient of variation of the compressive strength of concrete [4]

If the quality control is good during concreting, then the probability density function (PDF) of strength is expected to follow the normal distribution and the test results tend to cluster near to the average strength; the histogram of Fig. 1a is expected to be mesokurtic or leptokurtic (see Appendix for interpretation). The average strength and the mean strength coincides for normal distribution. If the test results are not symmetrical about the mean (i.e. skewness exists) then a statistical analysis that presumes normal distribution is misleading. The statistical analysis is the simplest if normal distribution for the strength is acceptable, as the normal distribution can be fully described mathematically by two statistical parameters: the mean strength and the standard deviation of the strength.

A sufficient number of tests is needed to accurately find the variation in concrete strength and to be able to use statistical procedures for interpreting the test results [5]. If only a small number of test results is available, the estimates of the standard deviation and the coefficient of variation become less reliable [6].

The magnitude of the variation in the strength of concrete in the structure is a result of quality control (over the concrete production, the transportation, the compacting and curing procedures, the specimen preparation and the laboratory testing of the specimens) [7, 8]. For existing structures, another source of variability is the influence of the environment, which may be uneven on the structure. However, for a selected set of constituent materials, the strength of concrete is basically governed by the water-cement (w/c) ratio. Further influencing parameters can be applied in more detailed analyses [9, 10].

Surface hardness test of concrete is typically performed in-situ on structural concrete members. The most important characteristic of the test is that the near-surface properties of the concrete in a structure are directly measured. It is not common in usual practice that parallel hardness tests are performed on moulded specimens as well, which are made from the concrete used in the structure; it can be the case only for pilot projects or research. For material research and device development the most common situation is, however, the exclusive use of moulded specimens tested under strictly controlled laboratory conditions.

During in-situ testing, the most significant characteristic of the non-destructive tests is that the compressive strength of the concrete is not measured in the structure. Instead, some other related properties are measured that are correlated to the compressive strength. It should be mentioned here that no scientific consensus exists for the term ‘hardness’ even for the definition of the word [11]. Also, specifically for the rebound hammer test, the possible relationship between concrete strength and hardness (both are time dependent properties) was only recently revealed, answering a 60 years old open question [12].

It is demonstrated in the technical literature that the average rebound index R_m(t) and the average compressive strength of concrete f_cm(t) – both are time dependent material properties – can not be directly correlated to each other as univariate functions; the relationship needs the introduction of the series of multivariate functions, where the independent variables are the degree of hydration, the type and amount of cement and aggregate, the environmental conditions and the testing conditions. The simplest construction of the series of the functions is introduced by the authors of present paper [12], where two independent variables were defined for the degree of hydration in terms of the water-cement ratio and time, and all the other influencing parameters were taken into account by empirical constants. The model was demonstrated to be a robust tool for the modelling of the rebound index R_m(t) vs. average compressive strength f_cm(t) relationship [13]. It was also demonstrated that the technical literature provided a wide range of rebound index vs. compressive strength relationships in the last 60 years that may generate concerns of the strength estimation. Based exclusively on the published literature data, one may erroneously estimate the concrete strength at certain rebound indices by a ±40-60 N/mm² variation. Results clearly demonstrated that the validity of particular proposals should be restricted to the testing conditions and the extension of the validity to different types of concretes or testing circumstances is impossible [14].

The uncertainty of the estimated compressive strength depends both on the variability of the in-situ measurements and the uncertainty of the relationship between hardness and strength. One must account for three primary sources of uncertainty for the estimate of the compressive strength of concrete by surface hardness test method [15]: 1) the uncertainty of the surface hardness test results; 2) the uncertainty of the relationship between concrete strength and the measure of surface hardness; 3) the variability of the concrete strength in the structure. The first source of uncertainty is associated with the inherent variability (repeatability) of the test method. The present paper provides information mostly to this topic. It should be emphasized that throughout the paper, the term repeatability and the illustrated standard deviation and coefficient of variation results are always indicating the variability of rebound indices at a test location and not the variability of averaged rebound indices at different test locations. Batch-to-batch variability and spatial variability analyses are outside the scope of the paper.

2. Significance of the study

The paper focuses on the statistical characteristics of different surface hardness test parameters that can be obtained by rebound hammer testing. The discussions cover both literature and own measurement data by Schmidt rebound hammer tests. The extensive statistical analysis of the variability of concrete rebound hardness parameters is made by a large database of 60 years laboratory and in-situ experience. The study covers several thousands of test locations providing more than eighty thousand individual rebound index readings that made possible to carry out detailed statistical analyses. It is demonstrated that several gaps are found both in current technical literature and standardisation. The paper intends to provide general and comprehensive data for the better understanding of the statistical characteristics of surface hardness of concrete. The reader can find the details of the devices and the historical review of their development as well as the most recent theoretical considerations in the technical literature and in selected papers of the authors [16-21].

3. Observational error for the rebound hammer test

The accuracy of statistical information is the degree to which the information correctly describes the phenomena that is intended to be measured [22]. It is usually characterized in terms of error in statistical estimates and is traditionally composed by bias (systematic error) and variance (random error) components. In statistics, sampling bias/sampling error is a deviated sampling during which sample is collected in such a way that some members of the population are less likely to be included than others. Problems with sampling are expected when data collection is entrusted to subjective judgement of human [22]. A biased sample causes problems because any statistical analysis based on that sample has the potential to be consistently erroneous. The bias can lead to an over- or underrepresentation of the corresponding parameter in the population. In statistics, inherent bias is a bias which is due to the nature of the situation and cannot, for example, be removed by increasing the sample size [22]. An example of inherent bias is the systematic error of an observer.

Systematic errors can lead to significant difference of the observed mean value from the true mean value of the measured attribute. Systematic errors are very difficult to deal with, because their effects are only observable if they can be removed. Such errors cannot, however, be removed by repeated measurements or averaging large numbers of results. A simple method to avoid systematic errors is the correct calibration: the use of the calibration anvil for the rebound hammers.

Random errors lead to inconsistent data. They have zero expected value (scattered about the true value) and tend to have zero arithmetic mean when a measurement is repeated. Random errors can be attributed either to the testing device or to the operator.

Fig. 3.         Scale of the rebound hammer

The observational error in the case of the rebound hammer test is due to the design of the scale of the device (Fig. 3). Its speciality is that no odd values are indicated on the scale. Therefore, the observer should decide during reading how the rounding of the read value is to be carried out. As the repetition of the readings is very fast in a practical situation, it is expected that the observer adds an inherent observational error to the readings of the rebound index, in favour of the even numbers. The existence of the phenomena was earlier indicated in particular publications for natural stones [23] and concrete [24] but was not analysed thoroughly.

To see the magnitude and the influence of such an observational error on the reading of the rebound index, a comprehensive data survey was carried out. A total number of 45650 rebound index readings was collected from 28 different sources. The data are based on both laboratory research and in-situ measurements. The rebound hammers were N-type original Schmidt hammers in all cases. The data are provided either by technical literature or from the data archives of the accredited testing laboratory of the BME Department of Construction Materials and Engineering Geology. This latter group of data is confidential for the protection of the buyers of the accredited testing laboratory, therefore, details of the structures or the concrete mixes used for particular measurements are not given in this paper.

	Total readings, N	Readings of even numbers, Neven	Readings of odd numbers, Nodd	Relative error, (Neven–Nodd)/N, %	Source of data
1	2160	1088	1072	+0.74%	laboratory
2	270	133	137	–1.48%	laboratory
3	120	62	58	+3.33%	in-situ
4	120	63	57	+5.0%	in-situ
5	1179	621	558	+5.34%	laboratory
6	1120	603	517	+7.68%	in-situ
7	7640	4189	3451	+9.66%	laboratory
8	510	284	226	+11.37%	in-situ
9	140	62	78	–11.43%	in-situ
10	1000	561	439	+12.20%	in-situ
11	2880	1623	1257	+12.71%	laboratory
12	5310	2999	2311	+12.96%	in-situ
13	200	113	87	+13.00%	in-situ
14	200	113	87	+13.00%	in-situ
15	3760	2151	1609	+14.41%	laboratory
16	990	570	420	+15.15%	in-situ
17	7560	4380	3180	+15.87%	laboratory
18	800	464	336	+16.00%	laboratory
19	70	41	29	+17.14%	in-situ
20	451	183	268	–18.85%	in-situ
21	460	276	184	+20.00%	in-situ
22	1070	644	426	+20.37%	laboratory
23	210	129	81	+22.86%	in-situ
24	1440	905	535	+25.69%	laboratory
25	2980	1873	1107	+25.70%	laboratory
26	1670	1102	568	+31.98%	laboratory
27	250	84	166	–32.80%	in-situ
28	1140	880	260	+54.39%	laboratory

 Table 1.

Statistical characteristics of the rebound index data: number of even or odd number readings and their relative error.

Table 1 summarizes the statistical characteristics of the rebound index data in terms of counting the even and odd number readings. It can be realized that the observational error may be significant. Over the complete field of the 45650 data points one can find 57.3% probability of even number readings and 42.7% probability of odd number readings. It should be noted here that the 45650 data points are the product of several different operators, therefore, no general statement can be taken about operator precision or measurement uncertainty. The unbiasedness of the data collection is highly dependent on the operator. It can be realized (without referring to the exact sources of the data) that the worst cases were corresponded to situations when unskilled/untrained users performed the tests (e.g. students with lack of long term practice in the use of rebound hammers). On the other hand, the best results were always corresponded to laboratory research or in-situ measurements performed by the skilled staff of the accredited testing laboratory of the BME Department of Construction Materials and Engineering Geology or by the staff of its predecessor institute (BME Department of Construction Materials).

From the practical point of view of material testing – and not from that of the requirements of analytical accuracy of probability theory – one may ask that how much is the influence of the observational error on the reliability of concrete strength estimation based on the rebound hammer test, as it is the most important aim in most of the cases when the rebound hammers are used. Strength estimation usually means the estimation of the mean compressive strength based on the mean rebound index (mean can indicate here either the average or the median value of the rebound index) and random errors are usually expected to have an influence on kurtosis rather than on the mean value.

The mostly erroneous dataset listed in Table 1 at the 28^th position is selected for the demonstration of an unfavourable performance. The dataset can be found in the technical literature (for the right of privacy of the original authors no reference is given here as the example is inferior). The test results were actually collected for a diploma thesis and the operator was the candidate undergraduate student (not at BME). The 1140 rebound index readings are the result of a test series conducted on 5 different concrete mixes where 20 replicate readings were recorded at 57 individual measuring locations. The overall statistical parameters of the strength measurements for the 5 mixes are as follows (in the order of f_cm, MPa; s, MPa; V, %): mix 1) 45.8 MPa; 7.48 MPa; 16.3%, mix 2) 48.3 MPa; 8.81 MPa; 18.3%, mix 3) 46.9 MPa; 1.03 MPa; 2.2%, mix 4) 34.3 MPa; 1.73 MPa; 5.1%, mix 5) 29.4 MPa; 2.38 MPa; 8.1%, that indicates a low level of quality control during the tests (compare to Fig. 2). The overall range is R_min = 20 and R_max = 51, for the rebound index readings. The resulted range of 31 shall not be criticised, as these readings are not of the same concrete. The average of the 880 even readings is R_m,even = 32.38 and the standard deviation of the 880 even readings is s_Rm,even = 3.80. The average of the 260 odd readings is R_m,odd = 32.18 and the standard deviation of the 260 odd readings is s_Rm,odd = 4.42. On the first look, these differences can be considered to be negligible. If one takes a look at a more detailed statistical parameter check then more reliable decisions can be taken. The reader can refer first to Fig. 4 where the 57 individual measuring locations are illustrated as R_m–f_cm (Fig. 4.a), as R_m–s_R (Fig. 4.b), and as R_m–V_R (Fig. 4.c) responses. 

Fig. 4. a)     Relationship between average rebound index and average compressive strength

Fig. 4. b)    Relationship between average rebound index and within-test standard deviation

Fig. 4. c)     Relationship between average rebound index and within-test coefficient of variation of 57 individual test locations

It can be realized that the dataset indeed covers values that confirm the above statement about the low level of quality control (the reader can compare Fig. 4.b and Fig 4.c with Fig. 11.a and Fig. 11.b). Further statistical considerations are illustrated in Fig. 5. The rebound index ranges of individual measuring locations are shown in Fig. 5.a, indicating with black tone the locations where the limit of 12 units suggested by ASTM C 805 is violated. The observational error is given in Fig. 5.b, which diagram shows the differences (in percents) between the only-even-number and only-odd-number averages calculated to each location. The deviation has a positive sign if the only-even-number average is higher and has a negative sign if the only-odd-number average is higher. It can be seen that the error can reach the magnitude of 20% at specific locations. Also, there are locations where zero number of odd readings was recorded and therefore the error is 100%.The diagram indicates these locations with a striped tone. It can be realized by the comparison of the two diagrams that the observational error and the inherent variance of concrete hardness are independent parameters, therefore, they can be separated and determined individually in theoretical analyses.

Fig. 5. a)     Range of rebound index of 57 individual test locations

Fig. 5. b)     Specific observational error of 57 individual test locations

It can be summarized as a conclusion that the observational error can be considerable in particular cases, but this error seems to have negligible influence when rebound indices are averaged. At the present stage of the research, it is not yet demonstrated if the observational error may result bias of the rebound index data. Future statistical analyses are needed to make clear the real influences. It is suggested, however, that a simple development of the testing device may eliminate the operator observational error: a scale of the index rider would be needed that indicates both even and odd values rather than only even values as it is the case for the original design. The currently available experimental results also demonstrate that the digital data collection of the coefficient of restitution (see e.g. the Silver-Schmidt hammer) instead of the operator’s eye sensory reading at the conventional rebound index (see e.g. the original Schmidt hammer) do not improve the precision of the measurement [25]. On the contrary: it has been shown on 10 different natural stones that the necessary sample size to arrive at the same confidence level of the estimation of the sample mean is considerably higher for the Silver-Schmidt hammer than is needed for the original Schmidt hammer, regardless the magnitude of the operator observational error [25]. It calls the attention to further future analyses before a proper possible improving development of the original Schmidt hammers; which devices are far the most successful non-destructive testing tools for the in-situ surface hardness testing of concrete as well as of natural stones.

4. Normality tests for the rebound hammer test

In mathematical statistics, normality tests are used to determine whether a data set can be modelled by normal distribution or not. The importance of the normality tests concerning the rebound hammer test can be understood since normality is an underlying assumption of many statistical procedures. There are about 40 normality tests available in the technical literature [26], however, the most common normality test procedures of statistical analyses are the Shapiro-Wilk test, the Kolmogorov-Smirnov test, the Anderson-Darling test and the Lilliefors test. It is demonstrated in the technical literature that the Shapiro-Wilk test is the most powerful normality test from the above four [27]. Present chapter focuses on statistical analyses based on the Shapiro-Wilk normality test.

Considering the rebound hammer test, one can assume that the rebound index reading sets of separate test locations are independent and identically distributed (i.i.d.) random variables since it can be supposed that the probability distribution of the rebound index does not change by location within the same concrete structure and the separate test locations can be considered to be mutually independent. Based on these assumptions, the central limit theorem applies for the rebound hammer test; i.e. the probability distribution of the sum (or average) of the rebound index reading sets of separate test locations (each with finite mean and finite variance) approaches a normal distribution if sufficiently large number of the i.i.d. random variables is available.

To see if the probability distribution of the rebound index reading set of an individual test location can be described by normal distribution or not, the Shapiro-Wilk normality test can be run. From 24 different sources, 4555 test locations were selected (from which 3447 of laboratory testing and 1108 of in-situ testing) where 10 individual rebound index readings were recorded at each location by N-type original Schmidt rebound hammer. The Shapiro-Wilk test was run to all data sets and the values for the W statistic was found to be in a wide range of W_min = 0.510 (p → 0) to W_max = 0.988 (p > 0.99) with a mean value of W_m = 0.885 (p = 0.145). Values of the W statistic follow a Beta probability distribution with strong negative skewness. It can be basically concluded that the hypothesis of normality can be accepted at very low levels of probabilities for individual test locations. From the analysis it can be realized that the hypothesis of normality can be accepted at 50% or lower probability in 87% of the cases. In 10% and 5% of the cases the hypothesis of normality can be accepted at 64% and 80% probability, respectively. The hypothesis of normality can be accepted at 95% or higher probability only in less than 2% of the cases.

It is not the aim of the authors to suggest if a triangular or a rectangular (uniform) probability distribution could be a better estimate for the rebound index reading set of an individual test location; future research is needed.

The practical application of the central limit theorem for the rebound index reading sets of individual test locations, however, may be a good indicator of the precision of the rebound hammer test. Two comparisons have been made in this sense. During the first one, literature data was analysed in which 36 individual, identical concrete cubes of 150 mm were tested by N-type original Schmidt hammer (with average compressive strength of f_cm = 29.6 MPa); recording 10 rebound indices on each cube [28]. Test results are considered to be rather accurate with an average rebound index of R_m = 36.9, with a standard deviation of the rebound index of s_R = 2.2 and a coefficient of variation of the rebound index of V_R = 5.9%. The practical application of the central limit theorem was the running of the Shapiro-Wilk test for 1, 2, 3, …, 36 rebound index reading sets combined. The expected behaviour is the value of the W statistic approaching unity by the increasing number of test locations combined. Fig. 6 summarizes the values of the W statistic as a function of increasing number of specimens included in the analysis. The value of the W statistic is approaching unity very fast, as it was expected.

Fig. 6.         W statistic of rebound index as a function of increasing number of specimens

During the second comparison, four different rebound indices were compared by the laboratory testing of 11 individual, identical concrete cubes of 150 mm (with average compressive strength of f_cm = 64.7 MPa). The testing devices were an L-type original Schmidt hammer, an N-type original Schmidt hammer and a first generation Silver-Schmidt hammer capable to record both R-values (conventional rebound index) and Q-values (square of the coefficient of restitution) (it should be noted here that the recently available second generation Silver-Schmidt hammers are no more capable to record the R-values). Table 2 summarizes test results. 20 rebound index recordings were taken by each device on each specimen. It can be seen that the highest precision corresponds to the N-type original Schmidt hammer (highest precision means here the lowest range and the lowest standard deviation for the measured values at individual test locations). Lower precision of the L-type original Schmidt hammer and of the Silver-Schmidt hammer is due to the lighter hammer masses impacting within both devices and the sensitivity of the electro-optical recording (Silver-Schmidt hammer).

Table 2.

Statistical characteristics of rebound indices obtained by different types of rebound hammers.

Fig. 7. W statistic of rebound index provided by different rebound hammers as a function of increasing number of specimens

The Shapiro-Wilk test was run in a similar way as of the first comparison. Fig. 7 summarizes the values of the W statistic as a function of increasing number of specimens combined. One can realize that values of W statistic approaches the fastest to unity for the N-type original Schmidt hammer due to its superior precision. In the case of the L-type original Schmidt hammer tendencies are similar, but the W statistic has lower values. Results are controversial in the case of the Silver-Schmidt hammer. Tendency of the values for the W statistic seem to decrease rather than increase, which contradicts probability theory and apparently indicates that the central limit theorem does not apply. The observed behaviour highlights the disadvantages of the electro-optical data collection. The results confirm the long term advantageous experiences with the N-type original Schmidt hammers (see e.g. [25] as well) and further appreciate – after more than 60 years – the original robust design of the device that provides superior precision compared to its competitors in use today.

5. Current standardisation of the rebound hammer test

Non-destructive testing methods for concrete structures require the statistical validation of the model parameters. In particular cases the formulation of the model is directly related to the statistical characteristics of the parameters considered. Laboratory and in-situ experiences have demonstrated that several material characteristics which are connected to the degree of hydration of hardened cement paste as well as of hardened concrete (i.e. modulus of elasticity, tensile and compressive strengths and surface hardness properties) may be modelled as random variables of normal probability distribution. There are, however, material properties for which the validity of the assumption of normal distribution can not be demonstrated or even no any indication is found in the technical literature considering an appropriate probability distribution. Numerical modelling or numerical simulations of concrete hardness behaviour need acceptable simplifications of the real behaviour. The current state of the standardisation of the rebound hammer test is summarized briefly in present chapter to be able to find the gaps in present knowledge and to provide a basis for the literature survey and a comprehensive analysis of the statistical characteristics of the rebound hammer test parameters given in further chapters of the paper.

The ISO 1920-7 International Standard and the EN 12504-2 European Standard specifies the method for determining the rebound index and the EN 13791 European Standard summarises guidance for the assessment of the in-situ concrete compressive strength in structures [29-31]. It is generally stated that the rebound hammer test of concrete is not intended to be an alternative to the compressive strength testing, but with suitable correlation, it can provide an estimate of the in-situ strength. Therefore, it can be supposed that the rebound hammer tests may provide alternative to drilled core tests for assessing the compressive strength of concrete in a structure if core test results can be obtained in limited number. Two different strength assessment procedures are described in EN 13791; both by the formulation of specific relationships between the in-situ compressive strength and the rebound indices. One alternative suggests the establishment of a relationship based on at least 18 drilled core strength results, while the other suggests the use of a basic curve, together with a shift of the basic curve, established by means of at least 9 drilled core strength results detailed in the standard. It is claimed that the basic curve has been set at an artificially low position so that the shift is always positive. The basic curve for the in-situ concrete compressive strength (f_c,is) is a bilinear relationship, f_c,is = 1.25×R – 23 (20 ≤ R ≤ 24) and f_c,is = 1.73×R – 34.5 (24 ≤ R ≤ 50), where R is the median value of the rebound index (acc. to EN 12504-2). Strength estimation without the direct calibration to drilled core strength results is not supported by the basic text of EN 13791.

National Annex of DIN EN 13791 suggests in its Table NA.2 numerical values according to which the rebound hammer method may be used singly under restricted conditions and the strength assessment can be performed by the suggested values [32]. The general idea is attributed to Manns and Zeus [33] and was adopted by CEN/TC 104/SC1 as well [34]. The suggested values are summarised in Table 3.

The ASTM C 805 International Standard contains precision statements for the rebound index of the rebound hammers [35]. It is given for the precision that the within-test standard deviation of the rebound index is 2.5 units, as “single-specimen, single-operator, machine, day standard deviation”. Therefore, the range of ten readings should not exceed 12 units (taking into account a k = 4.5 multiplier given in ASTM C 670). Dependence of the within-test standard deviation on the average rebound index is not indicated. Particular literature data support the ASTM C 805 suggestions, e.g. [36].

For the bias of the rebound hammer test no evaluation is given in the ASTM C 805 standard [35]. It is indicated that the rebound index can only be determined in terms of this test method, therefore, the bias can not be evaluated. This statement, however, in the point of view of the authors of present paper should be restricted to the Digi-Schmidt and the Silver-Schmidt type rebound hammers as only these models provide the rebound index readings digitally. The original Schmidt hammers have a sliding marker for the indication of the rebound index that shows the measured value over a scale on which only even numbers are indicated. The operator decides the reading based on his own judgement whether the reading is an odd or an even number. This sampling does not, therefore, exclude the possibility of existence of an observer error or an observer bias.

American Concrete Institute Committee 228 reapproved in 2003 the ACI 228.1R-03 Committee Report that covered implications on the statistical characteristics of the rebound hammer test; as an extension of ACI 228.1R-89 [15, 37]. No update has been made since then up today. The Report illustrated – on a basis of three literature references from the 1980’s – that the within-test standard deviation of the rebound index shows an increasing tendency with increasing average and the within-test coefficient of variation has an apparently constant value of about 10% (Fig. 8). Particular literature data contradicted the findings, e.g. [38]. The reader can realize that the information given in Fig. 8 is rather limited as well as apparently contradicts to an expected behaviour that can be postulated to be a similar trend that was shown in Fig. 2 for concrete strength. Number of data points indicated in Fig. 8 is only 55 and the range of the analysed rebound index is narrow and restricted to low values; all fall below rebound index of 35.

It can be realized that still several gaps can be found in the recommendations in terms of either limitations of the proposed methods or the missing statistical verification of the indicated numerical values. In the next chapters, these open questions are analysed without the aim of providing a complete solution for the topics discussed.

Fig. 8. a)     Within-test standard deviation of rebound index [15] 

Fig. 8. b)     Within-test coefficient of variation of rebound index [15] 

6. Statistical analyses of test parameters in view of current standardisation

6.1 Limitations for the use of basic curve of EN 13791

The idea of EN 13791 with the calibration of the rebound hammer tests to drilled core strength tests is a practical and undeniable method to overcome the concerns of strength assessment, however, it eliminates the advantages of the non-destructive method and technically turns back to the destructive testing. The main driver of the calibration is the relationship between the rebound index and the in-situ compressive strength obtained by drilled cores. It can be demonstrated that the development of a relationship based on 18 drilled cores and the corresponding rebound indices can result an acceptable confidence level for the strength assessment [6]. However, the use of the basic curve suggested in EN 13791 for the calibration by 9 drilled cores needs to be reconsidered.

Fig. 9. a) Empirical curves found in the technical literature between the rebound index and compressive strength.

Fig. 9. b) Experimental rebound index – compressive strength results (2658 test locations) together with the basic curve given in EN 13791.

Fig. 9.a indicates 40 empirical curves found in the technical literature for the assessment of concrete strength by the rebound hammer tests together with the basic curve given in EN 13791. Fig. 9.b indicates experimental results (2658 testing locations) collected from the technical literature and measured by the authors of present paper in the range of average rebound indices R_m = 12.3 to 58.6 and average compressive strengths of f_cm = 6.1 MPa to 105.7 MPa, together with the basic curve given in EN 13791. It can be realized that the basic curve is actually not set to an artificially lowest position for which always a positive shift could be applied for the actual strength assessment. Basic curve of EN 13791 is, therefore, suggested to be reconsidered. It may be also added that numerical values summarised in Table 3 according to the National Annex of DIN EN 13791 as well as of CEN/TC 104/SC1 N 295:1998 (claimed to be suitable for the rebound hammer test used singly for in-situ strength assessment) are located very close to the basic curve of EN 13791, therefore, do not always result conservative estimates either. Values given in Table 3 are suggested to be reconsidered.

Table 3.
Minimum median values of rebound indices corresponding to the strength classes [32-34].
Note: Bn and C classes indicated in the table are concrete compressive strength classification for normal weight concrete according to earlier German and recent European nomenclature, respectively.

In the followings a short numerical example is presented to highlight some antagonism hidden in the assessment methods suggested by EN 13791. Input data is taken from the technical literature [39]. Eighteen drilled cores were tested in compression and the corresponding average rebound index values (R_m,min = 22.2; R_m,max = 39.1) were also published along with the compressive strength values (f_c,min = 19.0; f_c,max = 41.0). Fig. 10.a. indicates the experimental results together with the basic curve of EN 13791 as well as the 10^th percentile curve that can be obtained from the basic curve by shifting according to the method described in EN 13791 Ch. 8.3 as Alternative 2 method [29]. If one uses the compressive strength results of the 18 drilled cores and assesses the strength class according to EN 13791 Ch. 7.3.2 (Approach A) then concrete strength class of C20/25 is resulted (where f_cm(n=18),is = 27.5 MPa, f_c,is,lowest = 19 MPa, s_is = 6.7 MPa, therefore, f_ck,is = 17.6 MPa > f_ck,is,nom = 17 MPa). If one, however, uses the 10^th percentile curve that was obtained from the basic curve by the shift and applies it to the actually recorded average rebound index values (i.e. estimates the in-situ compressive strength values by the acceptance of the 10^th percentile curve and supposes that the 18 average rebound index values are available from Schmidt hammer tests performed on the structure without preparing any more drilled cores) then completely different concrete strength class can be resulted: concrete strength class of C12/15 (where f_{cm(n=18),is,R} = 23.4 MPa, f_{c,is,lowest,R} = 9.2 MPa, s_is,R = 7.2 MPa, therefore, f_ck,is,R = 12.8 MPa > f_ck,is,nom = 10 MPa). If one deviates from the suggestions of EN 13791 and prepares the 50^th percentile curve rather than the 10^th percentile curve by shifting the basic curve and assesses the concrete strength class then C16/20 would be resulted. It can be concluded that the shape of the basic curve is not optimal and its use may result over-conservative strength estimation in certain cases. Coefficient of variation of the measured and the estimated compressive strengths may also indicate that the strength estimation is not powerful enough for the analysed case: V_c,is = 24.34% for the actually measured core strengths and V_c,is,R = 30.79% for the strengths estimated by the 10^th percentile curve. It is also possible to follow the suggestions of EN 13791 Ch. 8.2 (Alternative 1) for the analysed case and establish a specific relationship between the in-situ compressive strength and the rebound index result. For this example a best fit power function estimate was established in the form of f_c,is,R = 0.1474×R^1.521 of which regression coefficient was found to be R² = 0.82 and the 10^th percentile curve was set as shown in Fig. 10.b. If one assesses the strength class then C16/20 is resulted (where f_{cm(n=18),is,R} = 23.8 MPa, f_{c,is,lowest,R} = 12.9 MPa, s_is,R = 5.7 MPa, therefore, f_ck,is,R = 15.4 MPa > f_ck,is,nom = 14 MPa). It can be also demonstrated that the estimation is rather powerful: coefficient of variation for the estimated strengths becomes V_c,is,R = 23.86% that is almost equal to the coefficient of variation of the actually measured core strengths.

Fig. 10. a)   Experimental results of drilled cores together with the basic curve of EN 13791

Fig. 10. b)   Experimental results of drilled cores together with the best fit curve

6.2 Repeatability of the rebound hammer test as of ACI 228.1R

According to the ISO 3534-1 International Standard the repeatability is the precision under conditions where independent test results are obtained with the same method on identical test items in the same laboratory by the same operator using the same equipment within short intervals of time [40]. Reproducibility means the precision under conditions where test results are obtained with the same method on identical test items in different laboratories with operators using different equipment [40]. In the nomenclature of ACI 228.1R-03 Committee Report repeatability is referred as within-test variation and reproducibility is referred as batch-to-batch variation [15].

An extended repeatability analysis has been made on 8955 data-pairs of corresponding average rebound indices and standard deviations of rebound indices that were collected from 48 different sources (in which the number of in-situ test locations was 4785 and the number of laboratory test locations was 4170; resulting more than eighty hundred individual rebound index readings). Range of the studied concrete strengths was f_cm = 3.3 MPa to 105.7 MPa, and the range of the individual rebound indices was R = 10 to 63. The data are based on both laboratory research and in-situ measurements on existing buildings. The rebound hammers were N-type original Schmidt hammers in all cases. The data is provided either by technical literature or from the data archives of the accredited testing laboratory of the BME Department of Construction Materials and Engineering Geology. The averages and the standard deviations were calculated by 10 or 20 replicate rebound index readings on the same surface of a concrete specimen during laboratory tests, or at the same measuring area in the case of in-situ testing. The data were analysed to see the general repeatability (within-test variation) behaviour of the rebound hammer testing. Analysis of reproducibility (batch-to-batch variation) was not the aim of the authors. The range of the analysed data is from R_m,min = 12.2 to R_m,max = 59.0 for the averages and from s_R,min = 0.23 to s_R,max = 7.80 for the standard deviations. Coefficient of variation was also calculated and analysed. Range was found to be as from V_R,min = 0.43% to V_R,max = 31.12%.

Fig. 11.a shows the graphical representation of the statistical analysis considering the within-test variation as standard deviation over the average rebound index, while Fig. 11.b indicates the same but considering the within-test variation as coefficient of variation over the average rebound index. The reader can clearly realize that these parameters have similar tendency to that of the within-test variation of concrete strength has, as it was introduced earlier by Fig. 2; i.e. no clear tendency is found in the standard deviation over the average and a clear decreasing tendency can be observed in the coefficient of variation by the increasing average. Hence the implications given by the ACI 228.1R-03 Committee Report (Fig. 8) is suggested to be reconsidered.

Fig. 11. a)   Within-test standard deviation over the average rebound index 

Fig. 11. b)   Within-test coefficient of variation over the average rebound index 

6.3 Statistical parameter analyses connected to ASTM C 805

There are two underlying assumptions in the precision statements of the rebound index given in the ASTM C 805 International Standard: (1) the within-test standard deviation of the rebound index has a constant value independently of the properties of the actual concrete and of the actual operator error, and (2) the percentage points of the standardized ranges of N(m,1) normal probability distribution populations can be applied for the determination of the acceptable range of rebound index readings at test locations. No indication is given in the ASTM C 805 either about the probability distribution of the within-test standard deviation of the rebound index or about its percentile level for which the value is given in the standard. In the absence of the above information one may assume – as a first estimate – that the within-test standard deviation of the rebound index has a normal probability distribution and the value s_R = 2.5 is its mean value.

An extended statistical analysis has been made on the previously detailed 8955 data-pairs of corresponding average rebound indices and standard deviations of rebound indices that were collected from 48 different sources (in which the number of in-situ test locations was 4785 and the number of laboratory test locations was 4170). It can be realized in Fig. 12 that the distribution of the within-test standard deviation of the rebound index has a strong positive skewness (g = 1.7064), therefore, the assumption of the normal probability distribution should be rejected. Fit of distributions resulted that a three-parameter Dagum distribution (also referred in the literature as generalized logistic-Burr or inverse Burr distribution) gives the best goodness of fit out of more than 60 different types of distributions. The parameters of the distribution function are: a = 1.7958, b =3.7311, c = 1.2171.

Empirical mean value of the standard deviation of the rebound index is E[s_R] = 1.667; the median value is m[s_R] = 1.5; the mode value is Mo[s_R] = 1.45; the 95% percentile value is v₉₅[s_R] = 3.1526; for the analysed range of s_R = 0.23 to 7.80.

It can be realized that the s_R = 2.5 value does not coincide either with the mode, or the median (= 50th percentile), or the mean value, but rather corresponds to a p = 88.5% probability level. If one would estimate the probability distribution with a N(1.677, 0.75) normal distribution (for which the goodness of fit is considerably weaker than that of the Dagum distribution) then the s_R = 2.5 value would correspond to a p = 86.7% probability level.

Fig. 12. Relative frequency histogram together with the best goodness of fit three-parameter Dagum probability density function (PDF) of the standard deviation of the rebound index (s_R) corresponding to 8955 test locations


Next check can be the analysis of the rebound index ranges (r_R = R_max – R_min) at the test locations in the case of the real measurements. Fig. 13 indicates the empirical probability histogram together with the best goodness of fit four-parameter Burr distribution corresponding to 8342 test locations (in which the number of in-situ test locations was 4785 and the number of laboratory test locations was 3557). Note that the r_R analysis is based on a slightly smaller collection of data than that of the s_R analysis. In the technical literature several references include only the average rebound index and the standard deviation of the rebound index without providing the individual rebound index readings. That is the reason of the difference between the sizes of the examined databases. One can again realize a strong positive skewness (g = 1.9432). The parameters of the distribution function are: a=0.89001; b=4.0809; c=3.755; d=0.41591.

Empirical mean value of the range of the rebound index is E[r_R] = 4.8068; the median value is m[r_R] = 4; the mode value is Mo[r_R] = 3.75; the 95% percentile value is v₉₅[r_R] = 9; for the analysed range of r_R = 1 to 24.

Considering the value of r_R = 12 as of the ASTM C 805 proposal, a p = 98.7% probability level can be determined. The rebound index range at a test location corresponding to the p = 95% probability level as of the ASTM C 805 target is found to be r_R = 9.

Fig. 13. Relative frequency histogram together with the best goodness of fit four-parameter Dagum probability density function (PDF) of the range of the rebound index (r_R) corresponding to 8342 test locations

After the above statistical analyses that are only partly confirming the assumptions of ASTM C 805, the next check can be the analysis of the assumption of ASTM C 670 that actually suggests the application of the theory of standardized ranges (w = r/s) for N(m,1) normal probability distribution populations for the determination of the multiplier applied to the maximum acceptable range [41]. One may realize for the rebound hammer test (if 10 replicate readings are considered at each test location) that the suggested value of the multiplier is k = 4.5 according to ASTM C 670, which is the one-digit round value of the percentage point of the standardized range (w) for a sample of n = 10 from a N(m,1) normal probability distribution population corresponding to a cumulative probability of p = 95% (w = 4.474124; see e.g [42]). The standardized ranges usually can not be applied for actual measurements as the real standard deviation (s) is not known. Therefore, the studentized ranges (q = r/s) can be introduced for N(m,s²) normal probability distribution populations for the selection of the multiplier applied to the maximum acceptable range. Based on the number of the measured results an appropriate degree of freedom (n) for the independent estimate s² of s² should be selected. For large samples (n→∞) the percentage point of the studentized range (q) approaches to the percentage point of the standardized range (w). Fig. 14 indicates the cumulative distribution function of the calculated studentized ranges (q_R = r_R/s_R) corresponding to the 8342 test locations together with the percentage points of the standardized ranges for n = 10 of N(m,1) for cumulative probabilities of p = 0.01 % to 99.99% (based on [42]). It is assumed for the present analysis that the comparison of the empirical studentized ranges (q_R) with the standardized ranges (w) is acceptable due to the large number of measured data. It can be realized that the median (= 50th percentile) values are almost equal; for the empirical values of the studentized ranges q_R = 2.991 and for the standardized ranges by [42] w = 3.024202. It is demonstrated in the technical literature that the probability distribution of the standardized ranges (w) has a positive skewness (g = 0.3975), therefore the mean value E[w] does not equal to the median value, but E[w] = 3.077505 [42]. The probability distribution of the empirical studentized ranges (q_R) corresponding to the 8342 test locations, however, has a negative skewness (g = –0.26501), and the mean value is E[q_R] = 2.9794. Fit of distributions resulted that a four-parameter Pearson VI distribution (also referred in the literature as beta prime or inverse beta distribution) gives the best goodness of fit out of more than 60 different types of distributions. The parameters of the distribution function are as follows:  

where:

is the Euler Beta function

in which a = 41399.0, b = 27867.0, c = 35.186, d = –49.297

Fig. 14 clearly indicates the difference in the probability distributions of the standardized ranges (w) by [42] and that of the empirical studentized ranges (q_R) corresponding to the 8342 test locations. One can realize that the difference is considerable at the cumulative probability level of p = 95%; i.e. w = 4.474124 and q_R = 3.635.

As the selection of the analysed test locations was free of any filtering, it is assumed that further increase in the number of the data points would not result better fit between the probability distributions of the standardized ranges (w) and that of the empirical studentized ranges (q_R). Based on the present comprehensive statistical analysis, the application of Table 1 of ASTM C 670 for the rebound hammer test is suggested to be reconsidered.

Fig. 14. Cumulative probability distribution function (CDF) of the calculated studentized ranges (q_R = r_R/s_R) corresponding to 8342 test locations together with the standardized ranges (w) to n = 10 of N(m,1) for cumulative probabilities of p = 0.01 % to 99.99%.

7. Influences on the repeatability of the rebound hammer test

The relatively large number of data made possible to study the distribution of the repeatability parameters in further details. Considering the probability density function of the coefficient of variation of the rebound index, a strong positive skewness is realized again (g = 2.2472). Fit of distributions resulted that a three-parameter Dagum distribution gives the best goodness of fit out of more than 60 different types of distributions for the coefficient of variation of the rebound index readings. The parameters of the distribution function are: a = 2.2255, b =3.1919, c = 2.7573.

Empirical mean value of the coefficient of variation of the rebound index is E[V_R] = 4.4021%; the median value is m[V_R] = 3.8%; the mode value is Mo[V_R] = 3.125%; the 95% percentile value is v₉₅[V_R] = 9.2132%; for the analysed range of V_R = 0.43% to 31.12%.

The findings confirm experimental data available for the repeatability parameters of concrete strength [43, 44]. It was demonstrated in the literature – based on an extensive analysis of 10788 drilled core samples taken from 1130 existing reinforced concrete buildings – that the coefficient of variation of concrete strength had a lognormal probability distribution with strong positive skewness, while normal probability distribution was found for the compressive strength itself (conventional concretes were studied with compressive strength lower than 50 MPa; [44]). Similar observation can be made if one analyses the distributions of the standard deviation and the coefficient of variation of concrete strength indicated earlier in Fig. 2 in this sense (see Fig. 15).

Fig. 15.   Relative frequency histogram together with the best goodness of fit three-parameter Dagum probability density function (PDF) of the coefficient of variation of the rebound index (V_R) corresponding to 8955 test locations

From a reliability analysis point of view one may practically select the coefficient of variation as the parameter of repeatability for the rebound hammer test. For this purpose, however, the governing parameters over the changes of the coefficient of variation are needed to be known. The authors of present paper have analysed the available database, with the selection of the following possible influencing parameters: the w/c-ratios of the concretes, the age of the concretes, the cement types used for the concretes, the testing conditions of the concretes (dry/wet), the carbonation depths of the concretes and the impact energy of the rebound hammers (N-type original Schmidt hammer with impact energy of 2.207 Nm or L-type original Schmidt hammer with impact energy of 0.735 Nm).

For the analysis of the age of the concretes, 102 different concrete mixes were selected for which the development of the coefficient of variation was possible to be followed in time. The age of the tested concretes was between 1 day and 240 days. The measuring device was N-type original Schmidt hammer. All sources was laboratory studies, no in-situ measurements were available. The behaviour was found to be typical in each case, therefore, it was reasonable to prepare a smeared, unified response for all the 102 concrete mixes, apart from the differences in their compositions (Fig. 16). 

Fig. 16.       Coefficient of variation of the rebound index (V_R) in time

The following observations can be made. In the first 14 days a rapid decrease in the coefficient of variation is measured that is attributed to the fast hydration and the drying out of the tested surfaces. A minimum is reached in the coefficient of variation at the age of 28 to 56 days. The reason is the slowing down of the rate of hydration. Over 56 days of age a gradual increase is observed in the coefficient of variation attributed to the more and more pronounced influence of carbonation. The direct relationship between the depth of carbonation and the within-test coefficient of variation of the rebound index is discussed later in present paper.

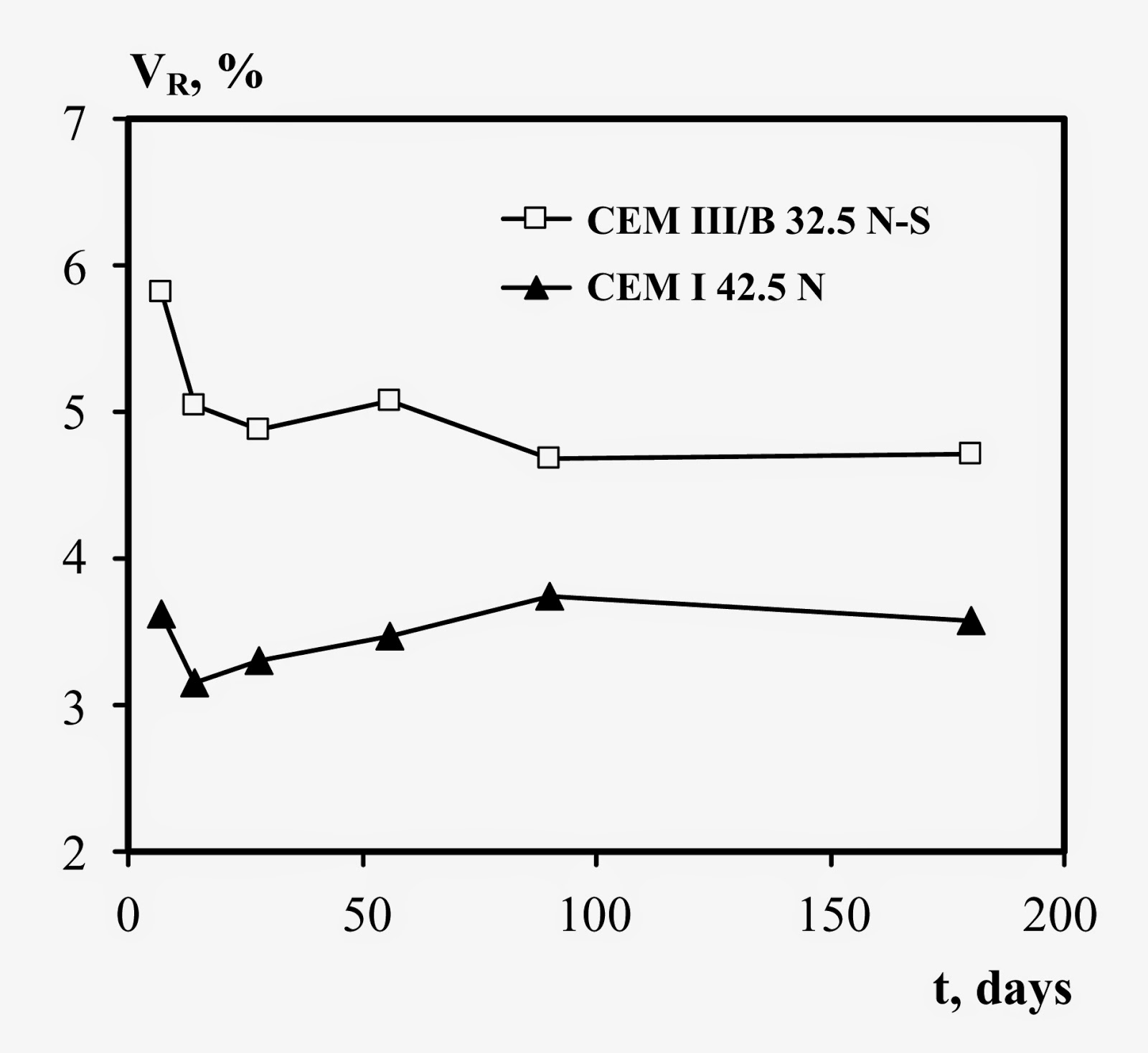
The 102 concrete mixes selected for the above analysis made possible to analyse the influence of the cement type on the repeatability parameters. Nine cement types were studied (in accordance with the designations used in EN 197-1 European Standard): CEM I 32.5; CEM I 42.5 N; CEM I 42.5 N-S; CEM I 52.5; CEM II/A-S 42.5; CEM II/A-V 42.5 N; CEM II/B-M (V-L) 32.5 N; CEM III/A 32.5 N-MS; CEM III/B 32.5 N-S. The influence of the applied cements was visible and robust (Fig. 17). It was found experimentally that the lowest coefficient of variation can be reached for the rebound index with the use of CEM I type Portland cements over the studied period of time. The coefficient of variation is increasing with decreasing the strength class of CEM I type Portland cements (not illustrated directly in Fig. 17). The use of blended cements (CEM II) or slag cements (CEM III) always resulted in higher coefficient of variation over the studied period of time, when compared to reference mixes made with Portland cements (CEM I). Differentiation between the influences of different hydraulic additives (fly ash to slag) for the blended cements (CEM II) or between the amount of slag applied for the slag cements (CEM III) was not possible due to the limited data available. Future research is needed in this field.

Fig. 17. Influence of the type of cement on the coefficient of variation of rebound index (V_R) in time

The influence of the water-cement ratio was possible to be studied for six types of cements with the analysis of the results of 93 different concrete mixes. The range of the studied water-cement ratios was w/c = 0.35 to w/c = 0.65. It was realized, that the coefficient of variation of the rebound index becomes lower if the water-cement ratio is decreased while all the other concrete technology parameters (including compacting) is unchanged.

As it was mentioned above, the carbonation was found to have a more pronounced influence on the repeatability of the rebound hammer tests on mature concretes, therefore, a targeted analysis was performed on mature concrete specimens of which age was 2 to 5 years during testing. 30 different mixes of concretes were selected for the analysis with the range of compressive strength of 42.6 to 91.7 MPa. The measured depths of carbonation were found to be between 2.2 mm to 22.8 mm. It was demonstrated that the coefficient of variation of the rebound index is higher for higher depths of carbonation (Fig. 18).

Fig. 18. Coefficient of variation of the rebound index (V_R) vs. average depth of carbonation (x_c)

The authors of present paper have found during their earlier in-situ testing experiences on masonry structures that the within-test standard deviation and the within-test coefficient of variation of the rebound index is very sensitive to the impact energy, therefore, a comparative study was performed on concretes using L-type and N-type original Schmidt hammers to reveal the existence of this influence for concretes as well. CEM 42.5 N type cement was selected and w/c = 0.40 – 0.50 – 0.65 water-cement ratios were applied for the same aggregate mix. In the concretes both the cement paste content and the consistency was set to be constant. The age of the test specimens was 3 to 240 days. It was demonstrated that both the standard deviation and the coefficient of variation of the rebound index is very sensitive to the applied impact energy before the age of 90 days. Experiments showed that the differences become more balanced and seem to disappear at ages over 90 days (Fig. 19).

Fig. 19. a)   Effect of the w/c ratio and the impact energy on the coefficient of variation of the rebound index in time, L-type original Schmidt hammer

Fig. 19. b)   Effect of the w/c ratio and the impact energy on the coefficient of variation of the rebound index in time, N-type original Schmidt hammer

8. Repeatability condition check according to EN 12390-3

There is considerable interest, from a practical point of view, on a possible connection of the repeatability of in-situ measurements (e.g. the rebound hammer tests) and that of the compressive strength tests: namely, it is an open question if the coefficient of variation of the rebound index (V_R) could be an acceptable estimate of the coefficient of variation of concrete compressive strength (V_f). Reliability analyses need the value of V_f, however, it is time consuming and expensive to establish its value in a practical situation. Rebound hammer test, on the other hand, is easy to perform and may provide a far less time consuming and expensive solution in a practical situation. Present chapter, therefore, illustrates own results in this field.

Laboratory tests were performed on 1350 concrete cubes of standard geometry on a wide range of water-cement ratios (w/c = 0.35 to 0.65) using nine different cement types detailed earlier in present paper. Rebound hammer tests according to [30] and compressive strength tests according to [45] were performed on two cubes of the same mix at the age of 1, 3, 7, 14, 28, 56, 90 and 180 days of age. The repeatability of the strength tests was calculated according to EN 12390-3 as the normalized range in percents: r_f = (f_c,max – f_c,min)/f_cm×100. Similarly, the normalized ranges in percents corresponding to the rebound hammer test results were formulated as: r_R = (R_m,max – R_m,min)/R_m,avg×100, where R_m,i is the average rebound index corresponding to each cubes and R_m,avg is the average of R_m,max and R_m,min.

The EN 12390-3 standard indicates that the precision of compressive strength testing (i.e. the repeatability of compressive strengths obtained on 150 mm cubes) is acceptable if r_f ≤ 9%. Regarding present tests, the value of r_f was found to be lower than 9% in 95.3% of the cases, with a mean of E[r_f] = 3.75% and a median of m[r_f] = 2.71% so the tests can be considered to be rather precise. No considerable influence of the age of concrete at testing was observed.

Fig. 20 indicates r_R and r_f in the same coordinate system at two different magnifications of the axes. One can clearly see that the two variables are completely independent from each other and no relationship is possible to be formulated between them. Therefore, it can be postulated that the coefficient of variation of the rebound index (V_R) could not be an acceptable estimate of the coefficient of variation of concrete compressive strength (V_f) in the proposed simplified way. If, however, the variation of the rebound index is considered in a different way than the coefficient of variation of test locations (e.g. by the adaptation of variograms to depict spatial variability in geostatistics [46-47]) then the rebound hammer test may be a suitable tool for the estimation of the coefficient of variation of concrete compressive strength (V_f) in a practical situation. Further research is needed in this field.

Fig. 20.     Precision (normalized ranges) of the compressive strength test (r_f,%) and rebound hammer test (r_R,%) indicating two different magnifications of the axes of the coordinate system.

9. Conclusions

An extensive statistical analysis of the variability of concrete rebound hardness parameters has been made based on a large database of 60 years laboratory and in-situ experience. The following conclusions can be drawn.

a)   The average rebound index R_m(t) and the average compressive strength of concrete f_cm(t) – both are time dependent material properties – can not be directly correlated to each other as univariate functions; the relationship needs the introduction of the series of multivariate functions, where the independent variables are the degree of hydration, the type and amount of cement and aggregate, the environmental conditions and the testing conditions.

b)   An observational reading error exists in the rebound hammer test due to the design of the scale of the device. The observational error can reach the magnitude of 20% in particular cases, but this error seems to have negligible influence when rebound indices are averaged. It is not yet demonstrated if the observational error may result bias of the rebound index data. It is suggested that a simple development of the testing device may eliminate the operator observational error: a scale of the index rider would be needed that indicates both even and odd values rather than only even values as it is the case for the original design.

c)    Normality tests demonstrated that the precision of the original N-type Schmidt hammer is superior to original L-type or Silver-Schmidt N-type hammers for concrete. Lower precision of the L-type original Schmidt hammer and of the Silver-Schmidt hammer is due to the lighter hammer masses impacting within both devices and the sensitivity of the electro-optical recording (Silver-Schmidt hammer).

d)   The basic curve of EN 13791 for the rebound hammer test is not set to an artificially lowest position for which always a positive shift could be applied for the actual strength assessment. Basic curve of EN 13791 is suggested to be reconsidered.

e)    The within-test variation (repeatability) parameters of the rebound hammer test have similar tendency to that of the within-test variation parameters of concrete strength; i.e. no clear tendency is found in the standard deviation over the average and a clear decreasing tendency can be observed in the coefficient of variation by the increasing average. ACI 228.1R-03 Committee Report implications contradict to these results, therefore, the within-test variation statements in ACI 228.1R-03 are suggested to be reconsidered.

f)     The probability distribution of the within-test standard deviation of the rebound index as well as of the rebound index ranges of individual test locations follow the Dagum distribution with strong positive skewness. ASTM C 805 implications can not fit to these findings, therefore the statements in ASTM C 805 about the values of the standard deviation and the range of rebound indices are suggested to be reconsidered.

g)   For the rebound indices, the probability distribution of the standardized ranges and that of the empirical studentized ranges are different and their values are about to be equal only at their mean value levels. At 95% probability level the difference is unacceptably high, therefore, the application of Table 1 of ASTM C 670 for the rebound hammer test is suggested to be reconsidered.

h)   The within-test coefficient of variation of the rebound index is influenced by the w/c-ratio of the concrete, the age of the concrete, the cement type used for the concrete, the testing conditions of the concrete, the carbonation depth of the concrete and the impact energy of the rebound hammer.

i)     The within-test coefficient of variation of the rebound index could not be an acceptable estimate of the coefficient of variation of concrete compressive strength, therefore, further research is needed to refine the rebound hammer test to become a suitable tool for the estimation of the variability of concrete compressive strength in a practical situation.

Authors hope that the results of the statistical analyses introduced in present paper may add to, further initiate and help the scientific progress of international scientific/technical committees, directly RILEM TC ISC “Non destructive in situ strength assessment of concrete”, ASTM Committee C09.64 “Nondestructive and In-Place Testing”, ACI Committee 228 “Nondestructive Testing of Concrete” and CEN/TC 104/SC1 “Concrete - Specification, performance, production and conformity”, throughout the database itself and the revealed characteristics of statistical parameters that can be a basis for further discussions.

Acknowledgements

Authors gratefully acknowledge the support of the project “Development of quality-oriented and harmonized R+D+I strategy and functional model at BME” (TAMOP-4.2.1/B-09/1/KMR-2010-0002), the project “Talent care and cultivation in the scientific workshops of BME” (TAMOP-4.2.2.B-10/1-2010-0009), the National Excellence Program “Elaborating and Operating an Inland Student and Researcher Personal Support System” (TAMOP 4.2.4. A/1-11-1-2012-0001) and the Hungarian Research Fund project “Durability and performance characteristics of concretes with novel type supplementary materials” (OTKA K 109233).

References

[1]  Masi, A., Chiauzzi, L. (2013) “An experimental study on the within-member variability of in situ concrete strength in RC building structures”, Construction and Building Materials, Vol. 47, October 2013, pp. 951-961.

[2]  ACI (2002) “Evaluation of Strength Test Results of Concrete”, ACI 214R-02, American Concrete Institute, Farmington Hills, Michigan, 20 p.

[3]  Teychenné, D. C. (1973) “Recommendations for the treatment of the variations of concrete strength in codes of practice”, Matériaux et Constructions, Vol. 6, No. 34, 1973, pp. 259-267.

[4]     fib Bulletin 3 (1999) “Structural Concrete – Textbook on Behaviour, Design and Performance”, Vol. 3, fédération internationale du béton (fib), December 1999, pp. 247-248.

[5]    Fiore, A., Porco, F., Uva, G., Mezzina, M. (2013) “On the dispersion of data collected by in situ diagnostic of the existing concrete”, Construction and Building Materials, Vol. 47, October 2013, pp. 208-217.

[6]   Carino, N. J. (1993) “Statistical Methods to Evaluate In-Place Test Results”, New Concrete Technology: Robert E. Philleo Symposium, ACI SP-141, T. C. Liu and G. C. Hoff, eds., American Concrete Institute, Farmington Hills, Michigan, pp. 39-64.

[7]    Neville, A. M. (1981) “Properties of Concrete”, Pitman, London, 532 p.

[8]    Nassif, A. Y., Petrou, M. F. (2013) “Influence of cold weather during casting and curing on the stiffness and strength of concrete”, Construction and Building Materials, Vol. 44, July 2013, pp. 161-167.

[9]   Popovics, S. (1987) “Model for the quantitative description of the kinetics of hardening of portland cements”, Cement and Concrete Research, Vol. 17, No. 5, September 1987, pp. 821-838.

[10]  Atahan, H. N., Oktar, O. N., Taşdemir, M. A. (2011) “Factors determining the correlations between high strength concrete properties”, Construction and Building Materials, Vol. 25, No. 5, May 2011, pp. 2214-2222.

[11]  Fischer-Cripps, A. C. (2000) “Introduction to Contact Mechanics”, Springer, New York, 2000, 243 p.

[12] Szilágyi, K., Borosnyói, A., Zsigovics, I. (2011) “Rebound surface hardness of concrete: Introduction of an empirical constitutive model”, Construction and Building Materials, Vol. 25, No. 5, May 2011, pp. 2480-2487.

[13]   Szilágyi, K., Borosnyói, A., Zsigovics, I. (2013) “Understanding the rebound surface hardness of concrete”, Journal of Civil Engineering and Management, Manuscript ID SCEM-2012-0173.R3 (in press)

[14] Szilágyi, K., Borosnyói, A. (2009) “50 years of experience with the Schmidt rebound hammer”, Concrete Structures, Vol. 10, 2009, pp. 46-56.

[15] ACI (2003) In-Place Methods to Estimate Concrete Strength, ACI 228.1R-03, American Concrete Institute, Farmington Hills, Michigan

[16]   Malhotra V. M., Carino N. J. (2004) “Handbook on nondestructive testing of concrete”, Second edition, CRC Press LLC, 384 p.

[17]  Bungey J. H, Millard J. H, Grantham M. G. (2006) “Testing of Concrete in Structures”, Taylor and Francis, New York, 352 p.

[18]  Szilágyi, K., Borosnyói, A., Dobó, K. (2011) “Static indentation hardness testing of concrete: a long established method revived”, Építőanyag, Vol. 63, No. 1-2, 2011, pp. 2-8.

[19]  Breysse, D. (2012) “Nondestructive evaluation of concrete strength: An historical review and a new perspective by combining NDT methods”, Construction and Building Materials, Vol. 33, August 2012, pp. 139-163.

[20]  Breysse, D., Editor (2012) “Non-Destructive Assessment of Concrete Structures: Reliability and Limits of Single and Combined Techniques”, State-of-the-Art Report of the RILEM Technical Committee 207-INR, Springer, 2012

[21]  Breysse, D., Fernández, J. L. M. (2013) “Assessing concrete strength with rebound hammer: review of key issues and ideas for more reliable conclusions”, Materials and Structures, July 2013, online article, 10.1617/s11527-013-0139-9

[22]   OECD (2008) “Glossary of Statistical Terms”, Organisation for Economic Co-operation and Development, 605 p.

[23]  Kolaiti, E., Papadopoulos, Z. (1993) “Evaluation of Schmidt rebound hammer testing: A critical approach”, Bulletin of the International Association of Engineering Geology, Paris, No.48, 1993, pp. 69-76.

[24]  Talabér, J., Borján, J., Józsa, Zs. (1979) “Preliminaries to the standardization of non-destructive tests in concrete technology”, Bulletin of the BME Department of Building Materials, Budapest, No. 29, 1979, 112 p. (in Hungarian)

[25]  Viles, H., Goudie, A., Grab, S., Lalley, J. (2010) “The use of the Schmidt Hammer and Equotip for rock hardness assessment in geomorphology and heritage science: a comparative analysis”, Earth Surface Processes and Landforms, Vol. 36., pp. 320-333.

[26] Dufour, J. M., Farhat, A., Gardiol, L., Khalaf, L. (1998) “Simulation-based Finite Sample Normality Tests in Linear Regressions”, Econometrics Journal, Vol. 1, pp. 154-173.

[27]  Razali, N. M., Wah, Y. B. (2011) “Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests”, Journal of Statistical Modeling and Analytics, Vol. 2, No. 1, pp. 21-33.

[28] BME (1981) “Introduction of the non-destructive testing methods to the quality assurance system of the 31 AEV precast company”, Research Report No. 206030, Budapest University of Technology, Department of Building Materials, Budapest, November 1981, 110 p.

[29] CEN (2007) “EN 13791:2007, Assessment of in-situ compressive strength in structures and precast concrete components”, European Standard

[30]  CEN (2012) “EN 12504-2:2012, Testing concrete in structures – Part 2: Non-destructive testing – Determination of rebound number”, European Standard

[31]  ISO (2004) “ISO 1920-7:2004, Testing of concrete - Part 7: Non-destructive tests on hardened concrete”, International Standard

[32]  DIN (2008) “DIN EN 13791:2008-05 Bewertung der Druckfestigkeit von Beton in Bauwerken oder in Bauwerksteilen; Deutsche Fassung EN 13791:2007”, German Standard

[33] Manns, W., Zeus, K. (1977) “Die nachträgliche Bestimmung der Betondruckfestigkeit”, Betonwerk + Fertigteil-Technik, Vol. 43, No. 8., August 1977, pp. 410-417.

[34]   CEN/TC 104/SC1 N 295:1998 “Assessment of in-situ compressive strength in structures and concrete components”, Unpublished manuscript

[35]   ASTM (2013) “Test Method for Rebound Number of Hardened Concrete”, ASTM C 805/C 805M – 13, ASTM International, West Conshohocken, Philadelphia, International Standard

[36]  Mommens, A. (1977) “La precision de l’estimation de la résistance du béton au moyen de l’indice sclérométrique”, Matériaux et Constructions, Vol. 10, No. 55, 1977, pp. 49-54.

[37]  ACI (1989) “In-Place Methods to Estimate Concrete Strength”, ACI 228.1R-89, American Concrete Institute, Farmington Hills, Michigan, 26 p.

[38]  Leshchinsky, A. M., Leshchinsky, M. Yu., Goncharova, A. S. (1990) „Within-Test Variability of Some Non-Destructive Methods for Concrete Strength Determination”, Magazine of Concrete Research, V. 42, No. 153, pp. 245-248.

[39]  Soshiroda, T., Voraputhaporn, K., Nozaki, Y. (2006) “Early-stage inspection of concrete quality in structures by combined nondestructive method”, Materials and Structures, March 2006, Vol. 39, No. 2, pp. 149-160.

[40]  ISO (2006) “ISO 3534-1:2006, Statistics – Vocabulary and symbols – Part 1: Probability and general statistical terms”, International Standard

[41]  ASTM (2013) “Standard Practice for Preparing Precision and Bias Statements for Test Methods for Construction Materials”, ASTM C 670 – 13, ASTM International, West Conshohocken, Philadelphia, International Standard

[42] Harter, H. L. (1960) “Tables of Range and Studentized Range”, The Annals of Mathematical Statistics, Vol. 31, No. 1960, pp. 1122-1147, 1960

[43]  Soroka, I. (1971) “On compressive strength variation in concrete”, Matériaux et Constructions, Vol. 4, No. 21, 1971, pp. 155-161.

[44]  Shimizu, Y., Hirosawa, M., Zhou, J. (2000) “Statistical analysis of concrete strength in existing reinforced concrete buildings in Japan”, Proceedings 12WCEE 2000: 12^th World Conference on Earthquake Engineering, January 30 – February 4, 2000, Auckland, New Zealand, No. 1499, pp. 1-8.

[45] CEN (2009) “EN 12390-3:2009, Testing hardened concrete– Part 3: Compressive strength of test specimens”, European Standard

[46]  Clark, I. (2001) “Practical Geostatistics”, Geostokos Limited, July 13, 2001, 120 p.

[47]  Breysse, D., Marache, A. (2011) “Some Estimates on the Variability of Material Properties”, in: Construction Reliability - Safety, Variability and Sustainability (Eds: Baroth, J., Schoefs, F., Breysse, D.), ISTE Ltd and John Wiley & Sons, Inc., 2011. pp. 77-96.

[48]   Student (1927) “Errors of Routine Analysis”, Biometrika, Vol. 19. No. 1-2, 1927, pp. 151-164.

Appendix

The term kurtosis (after the Greek word κυρτός = kurtos, meaning curved) is the measure of the peakedness of the probability density function of a random variable. The definition of kurtosis is originated to Pearson. In practice, the excess kurtosis is used, which gives a comparison of the shape of a certain probability distribution to that of the normal distribution. Normal distribution has zero excess kurtosis and is called mesokurtic. Probability distributions with positive excess kurtosis are called leptokurtic, and have a narrower peak around the mean and fatter (= longer) tails. Probability distributions with negative excess kurtosis are called platykurtic, and have a wider peak around the mean and thinner (= shorter) tails. The meaning of these words can be memorized by the instructive memoria technica given by Student (William Sealy Gosset) in his paper [48] (Fig. A.1): platykurtic distribution can be represented by a platypus, while leptokurtic distribution can be shaped by two kangaroos, noted for “lepping” (though, perhaps, with equal reason they should be hares as Student added in his paper) [48].

Fig. A.1. Memoria technica given by Student (William Sealy Gosset) in his paper [48] for the platykurtic and leptokurtic distribution.

In memoriam of our colleague, mentor and friend, 

István Zsigovics PhD, who has left us so early.

1949-2015
Dear István, thank you for everything.

May your soul rest in peace.

K. Szilágyi, A. Borosnyói